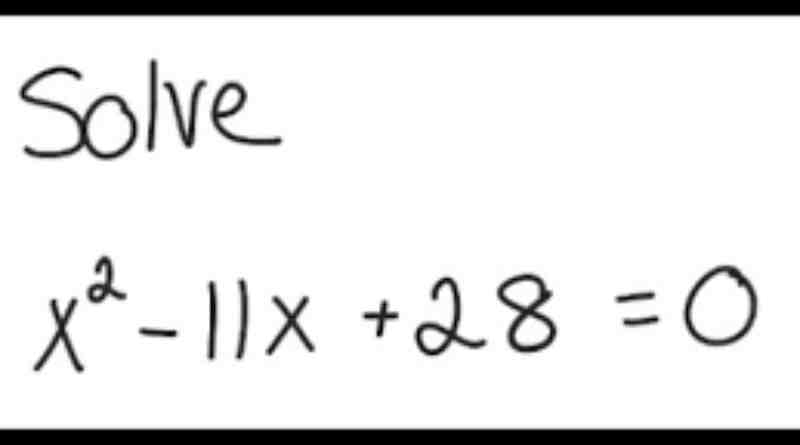Introduction
In the realm of mathematics, quadratic equations hold a significant place, offering a gateway to solving various real-world problems. Among the plethora of quadratic equations, one that often presents itself as both intriguing and challenging is x² – 11x + 28 = 0. In this comprehensive guide, we delve into mastering this quadratic equation, exploring its roots, principles, and methods for resolution.
Understanding the Quadratic Equation x² – 11x + 28 = 0
Before diving into the solving techniques, it’s imperative to understand the structure and significance of the quadratic equation at hand. The equation x² – 11x + 28 = 0 represents a second-degree polynomial equation, commonly known as a quadratic equation. Its format, ax² + bx + c = 0, encapsulates the essence of quadratic equations, where ‘x’ represents the variable, while ‘a’, ‘b’, and ‘c’ denote the coefficients.
In the equation x² – 11x + 28 = 0, the coefficients are as follows:
- ‘a’ = 1
- ‘b’ = -11
- ‘c’ = 28
Methods for Solving x² – 11x + 28 = 0
1. Factoring
Factoring stands as one of the primary methods for solving quadratic equations, especially those with easily factorable expressions. In the case of x² – 11x + 28 = 0, we aim to factor the expression into two binomials, equating their product to zero.
To factor x² – 11x + 28 = 0, we seek two numbers that multiply to give 28 and add to give -11, the coefficient of ‘x’. These numbers are -4 and -7. Hence, we rewrite the equation as (x – 4)(x – 7) = 0.
By setting each factor to zero, we derive the solutions:
- x – 4 = 0, which yields x = 4
- x – 7 = 0, which yields x = 7
Therefore, the solutions to the quadratic equation x² – 11x + 28 = 0 are x = 4 and x = 7.
2. Quadratic Formula
Another robust method for solving quadratic equations is employing the quadratic formula, which offers a systematic approach to finding the roots of any quadratic equation. The quadratic formula is expressed as:
�=−�±�2−4��2�
Applying the quadratic formula to x² – 11x + 28 = 0, we substitute the respective coefficients:
�=−(−11)±(−11)2−4⋅1⋅282⋅1
Solving further: �=11±121−1122 �=11±92 �=11±32
Thus, the solutions derived are:
- �=11+32=7
- �=11−32=4
Application and Relevance
Quadratic equations, including x² – 11x + 28 = 0, find extensive application in various fields, ranging from physics and engineering to economics and computer science. For instance, in physics, quadratic equations are pivotal in solving problems related to motion, such as projectile motion and harmonic oscillation.
Moreover, in economics, quadratic equations often model scenarios involving optimization and profit maximization. By mastering the resolution of quadratic equations, individuals equip themselves with indispensable tools for tackling real-world problems with confidence and precision.
Conclusion
In conclusion, mastering the resolution of quadratic equations, exemplified by x² – 11x + 28 = 0, empowers individuals with a fundamental mathematical skill set. Through methods like factoring and employing the quadratic formula, solving such equations becomes a systematic and intuitive process. Furthermore, understanding the application and relevance of quadratic equations underscores their significance across various domains. As we navigate the intricacies of quadratic equations, we pave the way for solving complex problems and advancing our understanding of the mathematical universe.
In essence, by unraveling the mysteries of quadratic equations, we embark on a journey of mathematical discovery and empowerment, where challenges transform into opportunities for growth and enlightenment.
Read also: check